长方体和正方体的体积课件人教版

这是一款关于长方体和正方体的体积的课件，很多数学老师都在使用，通过这个ppt可以更好进行讲课，和课程内容相互结合，学生更容易理解！

教学过程

一、什么是物体的体积

师：同学们看到这个课题，你觉得我们今天学习的重点和哪个关键词有关？（体积）（筛选信息的能力很强！）

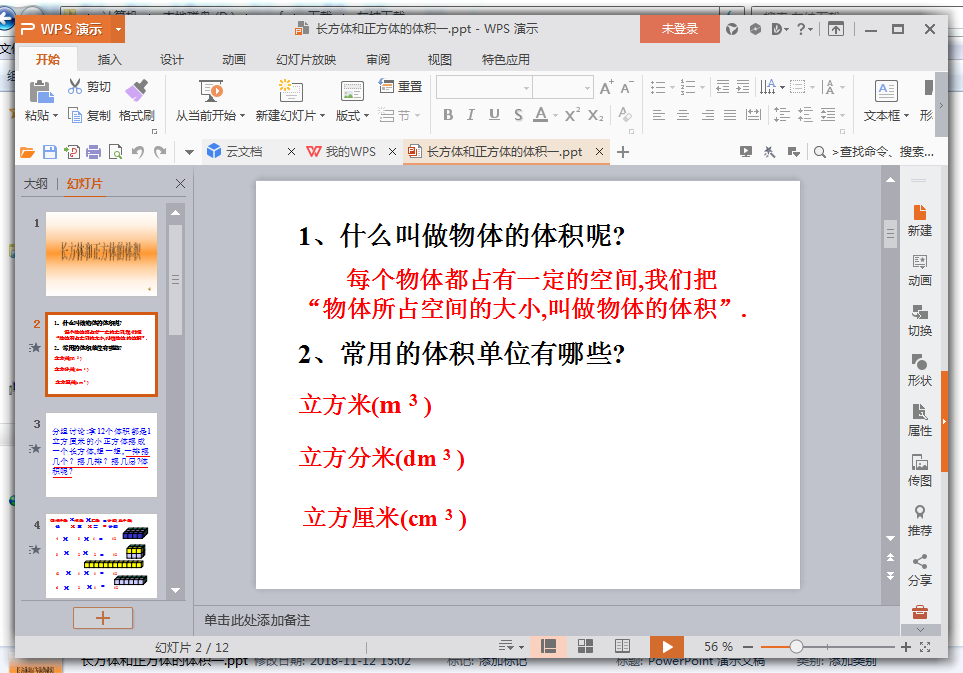
师：什么是物体的体积？

生：物体所占空间的大小叫做物体的体积。

师：物体所占的空间有大有小，为了方便比较，我们需要采用统一的体积单位来计量。

二、常用的体积单位及其定义

师：我们学过的体积单位有哪些？

生：立方厘米、立方分米、立方米。

课件出示：

棱长是1cm的正方体，体积是1cm3

棱长是1dm的正方体，体积是1dm3

棱长是1m的正方体，体积是1m3

师：1立方厘米有多大？（一个手指尖）1立方分米、1立方米呢？（一个粉笔盒的体积大约是1立方分米，讲台的体积大约是1立方米。）

师：我们在什么情况下用立方厘米做单位？什么时候用立方分米和立方米？比如计量橡皮擦的体积用（立方厘米），计量微波炉的体积用（立方分米），计量卡车集装箱的体积用（立方米）。是的，单位的选择要根据物体体积的大小来确定。

师：物体的体积大小，是由含有体积单位的多少来决定的。

三、长方体和正方体的体积公式

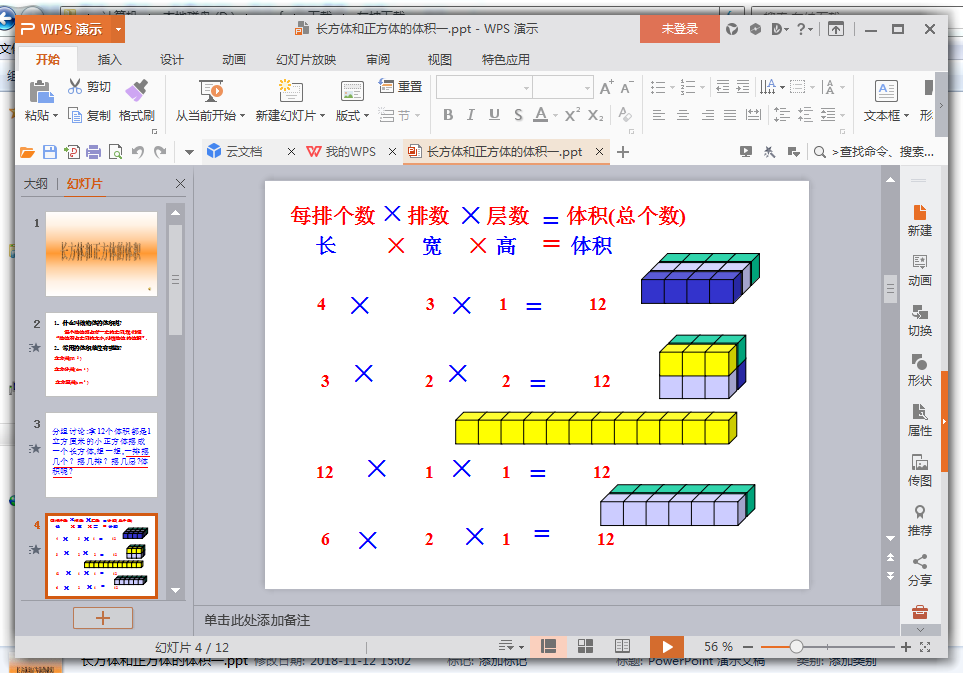
师：下面的图形是用棱长1cm的小正方体拼成的，请说出它们的体积各是多少？

课件出示：

①

②

③

师预先板书：

每行的个数行数层数数量（个）体积

师：为了让大家听得更清楚，请同学们在回答时按照这样的顺序来说明，先说每行的个数，再说行数和层数，最后说数量和体积，好吗？

生：①号图形每行有8个，只有1行，层数是1层，一共是8个，体积是8cm3

生：②号图形每行有4个，有两行，有一层，共有8个，体积是8cm3

生：③号图形每行有2个，有两行，有两层，共有8个，体积是8cm3

师：刚才同学们是怎样计算它们的体积的？

生：长方体的体积=长×宽×高（用字母表示：V=a.b.h）

师：韦老师想采访采访你，你是怎样界定长方体的长、宽、高的？是不是最长的那一条线段就叫做长？

生：我把左右方向的这条线段叫做长（即每行的个数），前后方向的这条线段叫做宽（也就是行数），上下方向的这条线段叫做高（即层数）。（结合学生的回答用课件进行展示）

师：当长方体的长、宽、高都相等时，这个长方体就变成了一个正方体，因为正方体的12条棱长度一样，所以我们把它统称为--棱长。

那么正方体的体积＝棱长×棱长×棱长（用字母表示：V=a.a.a）

四、基础练习：计算下面图形的体积。

师：光说不练假把式，下面我们就运用公式来求长方体和正方体的体积。

1.学生独立完成，教师巡视指导。

2.集体订正，发现问题及时纠正。

3.探索长方体和正方体的统一公式。

师：韦老师想问问大家，刚才你们在求长方体和正方体的体积时，第一步求的是什么？（在学生的算式上画出来）

生：长方体的底面积和正方体的底面积。例如8×4=32（平方厘米）是谁的的底面积？3×3=9（平方米）又是谁的底面积？

师：我听出来了，同学们的意思是在求长方体的体积或正方体的体积时，我们一般都是先求出它们的底面积，再用底面积乘高求得它们的体积，对吧？

师：那现在请同学们想想，长方体和正方体的体积公式是否可以合二为一？

生：长方体或正方体的体积=底面积×高（V=s.h）

师：也就是说，只要知道了底面积和高，就算不知道长和宽，也可以求出长方体或正方体的体积，是吗？

五、综合练习

师：要不我们一起去试试？

课件出示：只列式不计算（韦老师特别欣赏先看清楚题目要求再动笔的同学）

1.一根长方体柱子，底面积是0.6m2，高是5m，它的体积是多少立方米?

2.一根长方体木料，横截面积是0.08m2，长是5m，它的体积是多少立方米?

3.一根长方体蓄水池，底面积是10m2，深是5m，它最多能蓄水多少立方米?

4.一块长方体砖块，长24cm,宽12cm,厚是6cm，它的体积是多少立方厘米?

交流时强调（可利用教具进行演示说明）：

（1）“横截面积”和“底面积”

师：做完这四道题，同学们感觉第1、2、3题和第4题有什么不同？

生：第1、2、3题都是直接可以用底面积乘高，而第4题要先算出底面积，再用底面积乘高。

（2）“长”、“高”、“深”、“厚”（结合实物说明）

师：请同学们把这几个字读一读，看看你有什么感觉？

生：表达的方式不同，但是表示的意思一样。

六、变式练习

师：刚才大家都是直接运用公式进行正向计算，现在韦老师把条件改一改，看看你们还能不能那样应对自如？

1.一块长方体橡皮，横截面积是2cm2,体积是6cm3,它的长是多少厘米？

2.一块长方体集装箱，高是3m,体积是36m3,它的底面积是多少平方米？

3.一块长方体行李箱，长是8dm,宽是5dm,体积是240dm3,它的高是多少分米？

七、拓展延伸

1.用橡皮泥先捏成一个棱长是4厘米的正方体，然后再把这个正方体改捏成一个长方体，如果长方体的长是8厘米，宽是4厘米，那么它的高是多少厘米？

2.一个高40厘米，底面是正方体的长方体，如果高增加5厘米，表面积就增加80平方厘米，求原来长方体的体积。

八、全课总结

师：通过这节课的学习，你有什么体会或收获？

教学反思

《长方体和正方体的体积》这一课，我认为让学生亲眼看到，并亲自操作。通过合作自行探究总结结论。这样学生对知识掌握的会更牢固理解的更透彻。所以我在教学的过程中设计了“联系实际”“实际操作”“合作交流”等几个环节。

开始我利用粉笔盒、课本和长方体的橡皮擦等常见实物，从新认识并复习长方体的特点。然后分发学具让学生动手操作探究（小组合作）。我及时进行指点。这正是本册教材的重点，培养孩子们的空间观念，加强实际操作。通过实际观察、制作、拆拼等活动，学生轻松地掌握长方体体积计算公式的来源，并能够根据所给的已知条件正确地计算有关图形的体积。学生的动手操作能力也得到了提高。

通过这节课，也看出了很多课堂上的不足，在小组合作时，有几个孩子并没有认真地合作探究，如姜凯、郭俊宇他两个在合作探究时不听组长的，课下才知道他两个和组长发生过矛盾，所以课堂才会出现这一幕。今后的教学要避免这样的事情发生，做好学生的思想工作。要让他们在学习上保持最佳状态，让我的课堂达到高效。