百分数和小数分数的互化ppt教学免费下载

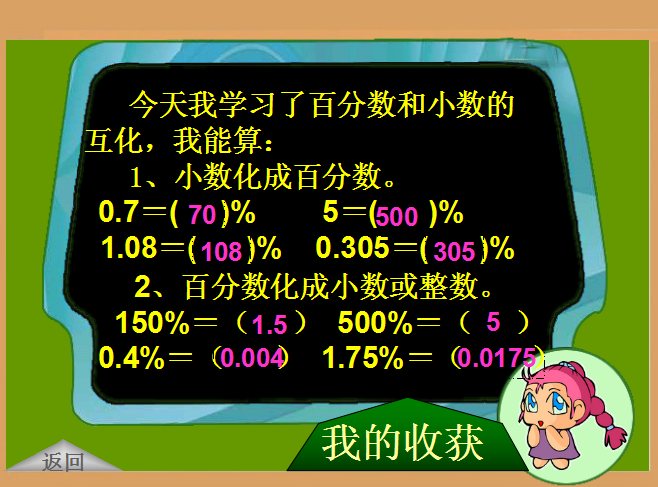
这个是老师专用的ppt模板，内容是百分数和小数分数的互化，里面的一些详情的内容都是可以写出来，并且可以自由的进行转换学习，可以修改更加好看的样式！

百分数和小数预览

数学公式记忆法

1. 用语言描述公式

比如我们前面描述向量的数量积公式“横坐标之积与纵坐标之积的和”，

再比如同底数幂相乘的公式，可直接描述为“底数不变，指数相加”，幂的乘方公式，可直接描述为“底数不变，指数相乘”。

可能这些还不足以简洁神奇，那么“奇变偶不变，符号看象限”，这聊聊十字，就概括了六组几十个诱导公式，简直是高中数学中的“神诀”，朗朗上口，轻松记忆，很多高中生毕业后，可能数学知识忘了，但这句口诀，终身难忘。

2. 抓住公式特征

比如两角和的余弦公式

公式特征相当明显，即两个余弦乘积减去两个正弦乘积，用谐音“科科减赛赛”或者“哭哭减笑笑”就很好记

再比如，一个不常用但一旦用了就很方便的公式

公式特征是“sin上面1-cos，或者sin下面1+cos”，根据这个特征，可谐音记作“山上一剑客，山下一侠客”，生动好记，还有些趣味。当然这些，都需要我们自己去琢磨这些公式的特征

3. 运用类比和比较记忆

比如上面两角和的余弦公式记住了，那么两角差的余弦公式可以类比记忆，

“哭哭加笑笑”，同时还可类比记忆两角和与差的正弦公式、正切公式，诸如此类

再比如，学过等差数列后，你熟悉了等差数列的性质，可以根据等比数列的定义，去理解记忆等比数列的性质，例如，等差数列的下标和如果一样，那么它们的和相等，到了等比数列这，就是它们的积相等了；

再如，等差数列前n项和有一个公式是n乘以中间项，那么类比到等比数列，可得相似结论：等比数列前n项积，等于中间项的n次方。诸如此类，类比在数列的学习中，是一种特别重要的思想

三. 掌握公式的推导

掌握公式的推导，不仅可以加深对公式的理解和记忆，还可以从公式的推导中学会一些数学方法。如二倍角公式，其实就是两角和的三角公式的一种特殊情况，

熟悉这样的推导过程，一方面加深对公式的理解，另一方面，你也更能体会赋值法的妙用

再比如，柯西不等式的推导（此公式教材不作要求，书中例题有，用向量方法很好推导，考试中一旦用起，会相当好用，如今年高考选择题16题）

熟悉这个推导过程，你不需要强记公式，理解了向量，自然就能写出来，另一方面，也能体会向量作为一种数学工具的强大作用

四. 灵活应用公式的方法和技巧

能灵活应用公式很重要，既要会顺用，也要会逆用，还要学会将公式变形后使用，这就把公式用活了，下面介绍部分公式的一些应用方法和技巧

1. 逆用公式

数学中的公式，其实都可以逆用，如阴阳两面，相辅相成。比如整式的乘法和因式分解，比如三角里的“辅助角公式”与“两角和与差的公式”，“二倍角公式”与“半角公式”的逆用推导，“和差化积”与“积化和差”之间的相互转化，等等

2. 公式变形

掌握一些恒等变形的规律，例如，余弦的二倍角公式，根据平方关系，可以推导出多种形式，结合题目需求灵活应用

3. 创造条件巧用公式

逆用、变形使用公式，其实就是创造条件，使用公式。在解题时，有些题目似乎不能用公式，但若对题目稍作变形，就能符合使用公式的条件，使问题巧妙地得以解决，如“三倍角公式”，本来看似陌生，但若先将2个角看作整体，再逐步展开，也就很好推导。再如三角中的很多“凑角”，让公式得以巧妙运用。

怎么学好百分数

1、首先调整心态，不要感觉百分数的知识点很难，这样的话在心里上就会有恐惧和排斥。

2、知识与技能:通过结合生活解决实际问题，体验百分数概念的形成过程，理解百分数的意义，掌握百分数的写法，了解百分数和分数在意义上的不同点。

3、过程与方法:在探究解决实际问题的过程中，培养学生合作交流的能力体会百分数所表示的两个数量的倍比关系，提高解决实际问题的能力及抽象概括能力。

4、情感态度与价值观:通过本课学习让学生体会百分数与社会的密切联系和在生活中的广泛应用，激发学习百分数意义的兴趣，理解百分数的意义以及与分数的区别和联系。

5、灵活把百分数化成小数、分数、折扣、成数。概念一定得背好。注意课前预习，否则上课时你会觉得内容难懂。解决问题时，要先寻找单位“1”，记住求单位“1”用除法，知道单位“1”用乘法。除不尽时要保留3位小数。